目次
https://1drv.ms/b/s!AivF3bzWXOzuhG1Xk5hscKYqkLkM
-------------------------------
今回は、OR・IE分野のゲーム理論について説明します。
これも実務で直接的に使う知識ではありませんが、意思決定を行う際に利用できる知識なので社会人であれば知っていて損はありません。
この分野について好きに書き始めると本が一冊出来上がりかねないので、今回は情報処理技術者で出題される可能性がある範囲に絞って説明します。
ゲーム理論は、複数のプレイヤーが存在する状況下において、最適な選択肢を選択するために使われる理論です。
主に「ゲーム木」と「利得表(利得行列)」を用いて状況を分析するのですが、情報処理技術者試験で集中的に出題されるのは利得表の方です。
とは言えゲーム木も出題される可能性があるので、簡単に説明します。
ゲーム木は、選択肢による分岐と各々の分岐で得られる利得を記述する方法です。
それぞれのプレイヤーが交互に意思決定を行う(相手がどの選択肢を選んだのかを見てから自分の選択肢を選べる)場面で有効な方法であり、例としては下記のように記述します。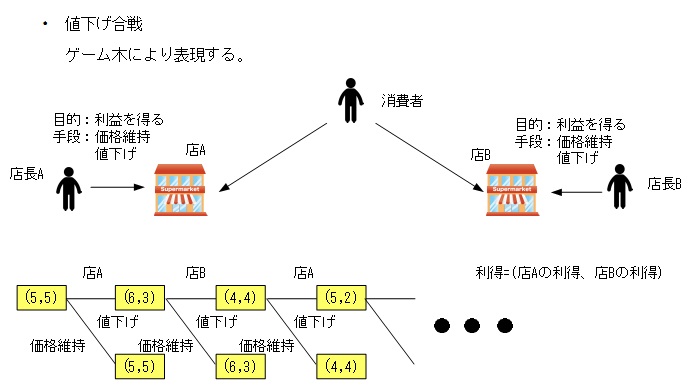
利得表は、各々のプレイヤーの選択肢の組み合わせと、各々の組み合わせの利得を表形式で記述する方法です。
それぞれのプレイヤーが同時に意思決定を行う(相手がどの選択肢を選んだのかわからない状態で自分の選択肢を選ぶ)場面で有効な方法で、例として下記のように記述します。

利得表から導き出せる戦略・状況としては、下記のようなものがあります。
もしかしたら下記にない戦略・状況が出題されるかもしれませんが、その場合は問題文中で何かしらの説明があるはずです。
(下記にない戦略・状況については、利得表外のパラメータが別途必要となるため)
- ナッシュ均衡
お互いに最適戦略(相手が選ぶ選択肢によらず、必ず他の選択肢よりも高い利得を得られる選択肢)が存在する場合に、お互いに最適戦略を採用する状態のことを指す。
この状態の時は、お互いに他の戦略を選択する動機が生まれず、状況が硬直化する。
例1ではお互いに最適戦略が存在するため、ナッシュ均衡の状態になる。
プレイヤーaの最適戦略はa1である。
(プレイヤーbがb1を選ぶ場合は、a1なら40、a2なら30の利得となりa1が優れる。プレイヤーbがb2を選ぶ場合は、a1なら50、a2なら25の利得となり、この場合もa1が優れる。)
また、プレイヤーbの最適戦略はb2である。
(プレイヤーaがa1を選ぶ場合は、b1なら20、b2なら30の利得となりb2が優れる。プレイヤーaがa2を選ぶ場合は、b1なら10、b2なら25の利得となり、この場合もb2が優れる。)
よって、a1とb2でナッシュ均衡となる。 - 純粋戦略
ある一つの選択肢を確定的に選ぶ戦略。
上記のナッシュ均衡の例で言うと、プレイヤーaはa1を選び続ける純粋戦略であり、プレイヤーbはb2を選び続ける純粋戦略である。 - ラプラス原理
相手の各選択肢の選択確率が不明の場合に、各々の選択肢が等確率で選ばれると仮定して期待利得を算出し、最も期待利得が高くなる選択肢を選択する。
例2において、プレイヤーbの戦略b1と戦略b2の選択確率が共に0.5であると仮定すると、戦略a1と戦略a2の選択確率は以下のようになる。例2ではどちらも期待利得が変わらないのでどちらを選んでも良い。
戦略a1…-15*0.5 + 20*0.5 = 2.5
戦略a2…5*0.5 + 0*0.5 = 2.5 - 期待値原理
相手の各選択肢の選択確率が予測できる場合に、各々の選択肢の選択確率を考慮して期待利得を算出し、最も期待利得が高くなる選択肢を選択する。
例2において、プレイヤーbの戦略b1の選択確率が0.8、戦略b2の選択確率が0.2であると仮定すると、戦略a1と戦略a2の選択確率は以下のようになる。この場合は戦略a2を選択するべきである。
戦略a1…-15*0.8 + 20*0.2 = -8
戦略a2…5*0.8 + 0*0.2 = 4 - 混合戦略
相手がどのように選択肢を選んだとしても、常に一定の期待利得を得らえるように一定の確率で各選択肢を選択する戦略。
例2においては、プレイヤーaは戦略a1を0.5、戦略a2を0.5の確率で選択することで、プレイヤーbがどのように選択肢を選択したとしても2.5の期待利得を得ることができる。また、プレイヤーbは、戦略b1を0.5、戦略b2を0.5の確率で選択することで、プレイヤーaがどのように選択肢を選択したとしても-2.5の期待利得を得ることができる。
混合戦略となる選択肢の選択確率を算出する方法としては、連立方程式を解く方法、微分を用いる方法等がありますが、試験では出題されないと思うので詳細は割愛する。
(仮に混合戦略が出題されたとしても、選択式問題なので算出方法を知らなくてもなんとかなります) - マクシミン原理
相手が自分にとって最も望ましくない(最も自分の利得が少なくなる)選択肢を選ぶという前提において、得られる利得が最も大きくなる選択肢を選択する。
損失を避けたい場合に採用する原理である。
例2において、プレイヤーaが戦略a1を選択した場合は、戦略b1が最も望ましくない選択肢であり、この場合のプレイヤーaの利得は-15である。戦略a2の場合は、戦略b2が最も望ましくない選択肢であり、この場合のプレイヤーaの利得は0である。よって、マクシミン原理に従うならプレイヤーaは戦略a2を選択するべきである。 - マクシマックス原理
相手が自分にとって最も望ましい(最も自分の利得が多くなる)選択肢を選ぶという前提において、得られる利得が最も大きくなる選択肢を選択する。
一般的には楽観的な原理であるとされているが、筆者の見解としては相手が選ぶ選択肢をコントロールできる場合に採用するべき原理であると考えている。
例2において、プレイヤーaが戦略a1を選択した場合は、戦略b2が最も望ましい選択肢であり、この場合のプレイヤーaの利得は20である。戦略a2の場合は、戦略b1が最も望ましい選択肢であり、この場合のプレイヤーaの利得は5である。よって、マクシマックス原理に従うならプレイヤーaは戦略a1を選択するべきである。